私です

すみません、出落ちです。

私のようなコピペプログラマにとって、他人が書いたソースコードを適当に自分用に変数を変えて切った貼ったした上、さも「私がやりました(ｷﾘｯ」と言う人は、 model.compile(以下略)を、 C言語を始めた人ががおまじないのように

#include <stdio.h>

int main(int argc, char *args[])
{
    printf("Hello, world!\n");
    return 0;
}

のように書いて、 includeで何？stdio.hって何？intって何？mainって何？argcって何？（以下略わからないけどとりあえずHello,World!って出るね！

みたいな感じで、分類問題なら

model.compile(optimizer=tf.train.AdamOptimizer(),loss='binary_crossentropy',metrics=['accuracy')

って書いてmodel.fit(train_x,train_y…)すれば学習して、model.predict(x,y,…)で予測できるんでしょ！

ってやってる人は多いかと思います。（いや、私だけ？） Adam等はさておき、cross entropyについて、理解したつもりになったのでこちらにて。

cross entropyって何？

さて、cross entropyって何？という話で、

負の対数尤度関数 (Negative Loglikelihood Function）
交差エントロピー誤差関数ともいう

らしいです。なんのこっちゃ。

数式は以下の通りです。(binary cross entropyの場合)

$\displaystyle E = -\sum_{i=1}^N \left( t_i \log y_i + (1 - t_i ) \log ( 1 - y_i )\right)$

なんのこっちゃ。

cross entropyは分類問題を0～1の連続値で返してほしいときに使うので、二値問題で考えてみましょう。

二値分類問題なので、あるデータを与えられたとき、それが0なのか、1なのかを判別します。 (多値分類問題もone-hot化＆softmaxするので、各値が1(True)なのか0(False)なのかの程度を返すので同じですが)

さてもう一度、先程の数式。

$\displaystyle E = -\sum_{i=1}^N \left( t_i \log y_i + (1 - t_i ) \log ( 1 - y_i )\right)$

yが予測結果でtが真の値です。予測する対象が一つ(オンライン処理)であればΣが不要なので、こうなります。

$\displaystyle E = -\left( t \log y + (1 - t) \log ( 1 - y )\right)$

さて、ここで二値分類なのでyは0～1を、tは0か1が入ってきます。 tが0の場合と、tが1の場合で、それぞれyを0～1へ推移させた場合、Eはどのような推移をしていくのかを見てみましょう。

import numpy as np
from matplotlib import pyplot as plt

# yの値を0(.00001)～1に推移
y = np.arange(0.00001,1,0.00001).reshape(-1,1)

# T=0をyの配列分用意
t_0 = np.zeros(y.shape[0]).reshape(-1,1)
# T=1をyの配列分用意
t_1 = np.ones(y.shape[0]).reshape(-1,1)

# np.logをそのまま使うとnp.log(0)のとき発散してしまうので、最小値を1e-100に固定
log = lambda x:np.log(np.clip(a=x, a_min=1e-100, a_max=x))

# 交差エントロピー誤差関数(公式通りsumしておく)
cross_entropy = lambda t,y: np.sum(-t*log(y)-(1-t)*log(1-y),axis=1)

# エントロピーの値をそれぞれ出す
E_0 = cross_entropy(t_0,y)
E_1 = cross_entropy(t_1,y)

# 描画
plt.figure()
plt.plot(y,E_0,c='red',label = "T=0")
plt.plot(y,E_1,c='blue',label = "T=1")
plt.xlabel("y")
plt.ylabel("E")

f:id:kazuhitogo:20181101150608p:plain

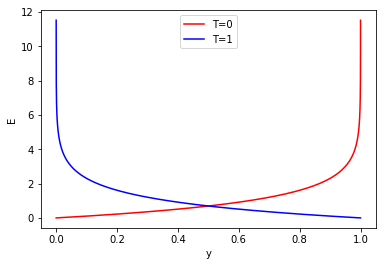
これを見ると、値が遠ければ遠いほどものすごく大きい値を返す(T-y=|1|のときは発散する)ことがわかります。すなわち間違いが大きい場合は誤差Eも跳ね上がるし、近ければ誤差は少ないよ、ということです。

学習して学習して、そしてこの誤差を0に出来たとき人は幸せになれるわけです。

で、0にするにはwとbをいじって0になる値を探すわけですが….。

それを数学的に解くのは難しいので、

微分してその刹那wやbをどっちにどれくらいずらせば良い方向に行くのかを計算
実際にずらす

を繰り返して、最適なwとbを探すのがニューラルネットの学習方法なわけですね。

なのでEをwとbでそれぞれ偏微分してどれくらいwとbをずらせばよいのか計算しましょう。 Eの式にwは含まれないので一旦yをはさみます。

$\displaystyle \frac{dE}{dw} = \frac{dE}{dy}\frac{dy}{dw}$

さて、 $\displaystyle E = -\left( t \log y + (1 - t) \log ( 1 - y )\right)$ でしたので、対数関数の微分は対数の関数を分数に持っていけばよいので（高校数学ですね！）、

$\displaystyle \frac{dE}{dy} = \frac{t}{y} - \frac{1-t}{1-y}$

ですね。

それを先程の式に当てはめると、

$\displaystyle \frac{dE}{dy}\frac{dy}{dw} = -(\frac{t}{y} - \frac{1-t}{1-y})\frac{dy}{dw}$

となります。

さて、yをwで微分ですが、二値分類で確率の出力をしている前提の話ですので、出力層の活性化関数はsigmoid関数を使っているはずです。

sigmoid関数は

$\displaystyle y = \frac{1}{1+e^{-z}}$

の通りなので、 zにwx + bを入れ、

$\displaystyle y = \frac{1}{1+e^{-wx-b}}$

となります。 …

…

微分の仕方忘れたので、ここからパクリます。これをwで微分すると、

$\displaystyle \frac{dy}{dw} = y(1-y)x$ となります。

さて、合わせるとこうなります。

$\displaystyle \frac{dE}{dy}\frac{dy}{dw} = -(\frac{t}{y} - \frac{1-t}{1-y})(y(1-y)x)$

texを書くの疲れてきたので、整理を省略すると、

$\displaystyle \frac{dE}{dy}\frac{dy}{dw} = -(t-y)x$

となります。

エントロピーを小さくするためにどれくらいずらしたのか、を計算した結果が、 - (真の値 - 予測の値) * xになってしまうんですね。これをwに加算して、再度学習すればよいわけです。

同様のことをbについても行うと、

$\displaystyle \frac{dE}{db}=-(t-y)$

となり、こちらもほぼ同様な(真の値 - 予測の値)になります。これをbに加算して（以下略

ちなみにこのような美しい数式になるのは、誰かが楽に計算したいがために、このような数式を見つけ出したのでしょう。 …たぶん。

さて、これを持って学習を可視化してみましょう。

データが多すぎると大変なので、ANDゲートをロジスティック回帰で解く問題としてみましょう。 (((1,1)が1,(0.0),(0,1),(1,0)が0と返すようになればOK)

%matplotlib nbagg
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.animation as animation
rs = np.random.RandomState(4545)

# tは正解,yは予測結果
cross_entropy = lambda t,y: np.sum(-t*log(y)-(1-t)*log(1-y))

# np.logをそのまま使うとnp.log(0)のとき発散してしまうので、最小値を1e-100に固定
# cross_entropy関数で使う
log = lambda x:np.log(np.clip(a=x, a_min=1e-100, a_max=x))

# 活性化関数sigmoid
sigmoid = lambda x: 1.0 / (1.0 + np.exp(-x))

# 予測結果
predict = lambda w,b,x:sigmoid(np.matmul(w,x)+b)

# データ
train_x = np.array([[0,0],[0,1],[1,0],[1,1]],dtype=float)
train_y = np.array([0,0,0,1])

# w,bの初期化
w = np.array([1.0,1.0])
b = 1.0
# 学習率
e = 0.05
# 可視化用履歴変数
w_hist = []
b_hist = []
i_hist = []
y_hist = []
cost_hist = []
w_hist.append(w)
b_hist.append(b)
dw = np.zeros(2,dtype=float)
db = 0.0
# epoch数
epoch = 40
for j in range(epoch):
    # 学習順序ガチャ
    learn_order = rs.choice(np.arange(train_x.shape[0]),train_x.shape[0],replace=False)
    for i in learn_order:
        t = train_y[i]
        x = train_x[i]
        y = predict(w,b,x)
        cost = cross_entropy(t,y)
        delta = -(t-y)
        dw = e * delta * x
        db = e * delta
        w = w - dw
        b = b - db
        i_hist.append(i)
        w_hist.append(w)
        b_hist.append(b)
        y_hist.append(y)
        cost_hist.append(cost)

# wx + bの線履歴を計算
x0_hist = [-3,3]
x1_hist = np.zeros(len(w_hist)*2).reshape(len(w_hist),2)
for i in range(len(w_hist)):
    x1_hist[i,0] = -(w_hist[i][0]/w_hist[i][1])*x0_hist[0] - b_hist[i]/w_hist[i][1]
    x1_hist[i,1] = -(w_hist[i][0]/w_hist[i][1])*x0_hist[1] - b_hist[i]/w_hist[i][1]

def update_fig(i):
    print(i)
    plt.cla()
    plt.xlim(-1,2)
    plt.ylim(-1,2)
    plt.scatter(train_x[:,0],train_x[:,1])
    # 線を引く
    plt.plot(x0_hist,x1_hist[i],c='black')
    plt.scatter(train_x[i_hist[i],0],train_x[i_hist[i],1],c='red')
    # cost表示
    plt.text(-0.5, -0.5, str(cost_hist[i]))
    
    if i < 4000:
        # 修正後の線を引く
        plt.plot(x0_hist,x1_hist[i+1],c='red')
    for i,(x,y) in enumerate(zip(train_x[:,0],train_x[:,1])):
        plt.annotate(str(train_y[i]),(x,y))
    
    
fig = plt.figure(figsize = (6, 6))
anim = animation.FuncAnimation(fig,update_fig,interval=10,frames=len(w_hist))